Metal Weight Calculator

The Metal Weight Calculator is an online tool designed to determine the weight of various metals such as stainless steel, aluminum, and brass, across different shapes. Ideal for professionals in industries such as construction, manufacturing, and logistics, this calculator simplifies the process of estimating metal weights with accuracy. 

How to Use the Metal Weight Calculator?

 The Metal Weight Calculator simplifies the process of estimating the weight of various metals across different shapes. Follow these steps to accurately calculate the mass of your metal components:

Principles of Calculation

The Metal Weight Calculator utilizes basic geometric principles to determine the volume of the metal shapes and then multiplies it by the density of the selected metal to calculate its mass. The formula used is:

$$ \text{Mass} = \text{Volume} \times \text{Density} $$

Input Parameters

1. Metal Options: Select the type of metal from the provided options, including Stainless Steel, Aluminum, and Brass. This choice will determine the density value used in the calculation.
2. Shape Options: Choose the shape of the metal component from the dropdown menu. Available options include Rectangular, Circular, Hexagonal, Octagonal, Ring, Wire, and Tube.
3. Dimensions: Based on the selected shape, input the following parameters:
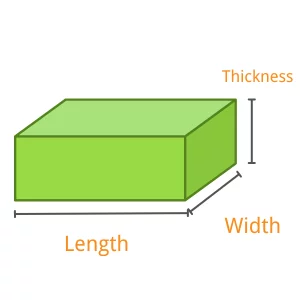
   • For Rectangular: Length, Width, Thickness, Number of Metal
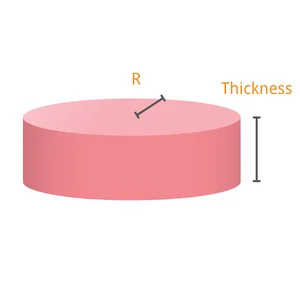
   • For Circular: Radius, Thickness, Number of Metal
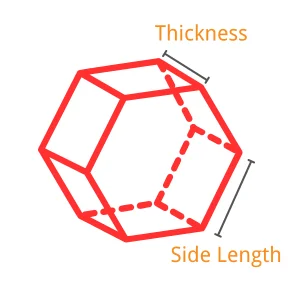
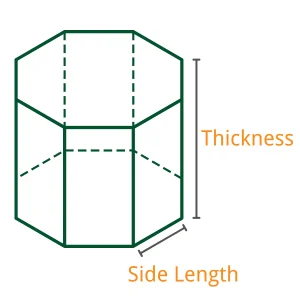
   • For Hexagonal and Octagonal: Side Length, Thickness, Number of Metal
   • For Ring: Inner Radius, Outer Radius, Thickness, Number of Metal
   • For Wire: Wire Radius, Length, Number of Metal
   • For Tube: Inner Radius, Outer Radius, Length, Number of Metal

Calculation Formulas

Rectangular:

$$ \text{Volume} = \text{Length} \times \text{Width} \times \text{Thickness} \times \text{Number of Metal} $$

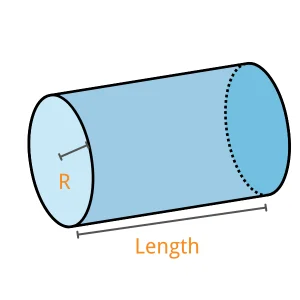
Circular:

$$ \text{Volume} = \pi \times \text{Radius}^2 \times \text{Thickness} \times \text{Number of Metal} $$

Hexagonal:

$$ \text{Volume} = \left( \frac{3 \sqrt{3}}{2} \right) \times \text{Side Length}^2 \times \text{Thickness} \times \text{Number of Metal} $$

Octagonal:

$$ \text{Volume} = \left( 2 + 2 \sqrt{2} \right) \times \text{Side Length}^2 \times \text{Thickness} \times \text{Number of Metal} $$

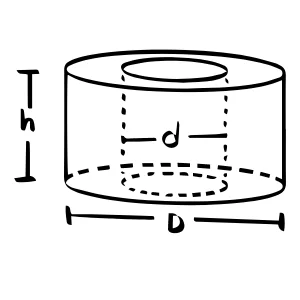
Ring:

$$ \text{Volume} = \pi \times (\text{Outer Radius}^2 - \text{Inner Radius}^2) \times \text{Thickness} \times \text{Number of Metal} $$

Wire:

$$ \text{Volume} = \pi \times \text{Wire Radius}^2 \times \text{Length} \times \text{Number of Metal} $$

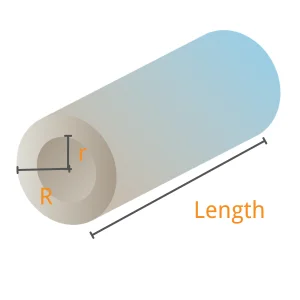
Tube:

$$ \text{Volume} = \pi \times (\text{Outer Radius}^2 - \text{Inner Radius}^2) \times \text{Length} \times \text{Number of Metal} $$